Eigenschappen van een gelijkbenige driehoek

Een driehoek waarvan de twee zijden gelijk zijnwordt gelijkbenoemd genoemd. Deze zijden worden lateraal genoemd en de derde zijde wordt de basis genoemd. In dit artikel zullen we je vertellen over wat de eigenschappen zijn van een gelijkbenige driehoek.

Stelling 1

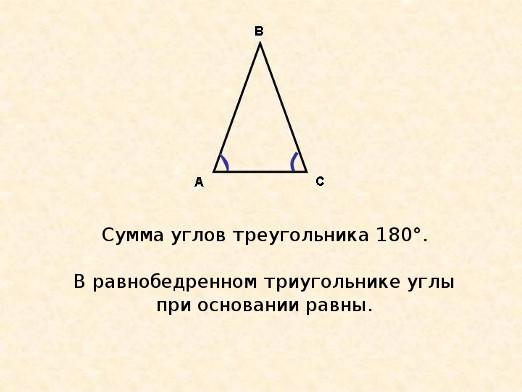
Hoeken nabij de basis van een gelijkbenige driehoek zijn gelijk aan elkaar

Bewijs van de stelling.

Stel dat we een gelijkbenige driehoek hebbenABC, waarvan AB de basis is. Laten we naar de BAC van de driehoek kijken. Deze driehoeken zijn bij het eerste teken gelijk aan elkaar. Zo is het, omdat BC = AC, AC = BC, hoek ACB = hoek van ACB. Hieruit volgt dat de hoek BAC = de hoek ABC, omdat dit de hoeken zijn van onze gelijke driehoeken. Hier is de eigenschap van de hoeken van een gelijkbenige driehoek.

Stelling 2

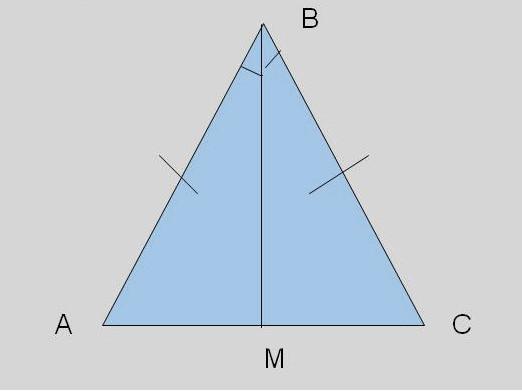
De mediaan in de gelijkbenige driehoek, die naar de basis werd gedragen, is ook de hoogte en bisectrix

Bewijs van de stelling.

Stel dat we een gelijkbenige driehoek hebbenABC, waarvan de basis AB is, en CD is de mediaan die we naar de basis hebben geleid. In de driehoeken ACD en BCD is de hoek CAD = de CBD-hoek, als de corresponderende hoeken aan de basis van een gelijkbenige driehoek (stelling 1). En de kant AC = kant BC (door de definitie van een gelijkbenige driehoek). Zij AD = zijde BD, nadat punt D het segment AB in gelijke delen verdeelt. Dit betekent dat de driehoek ACD = driehoek BCD.

Van de gelijkheid van deze driehoeken die we hebbengelijkheid van de hoeken. Dat wil zeggen, de hoek ACD = de hoek van de BCD en de hoek ADC = de hoek van de BDC. Uit gelijkheid 1 volgt dat CD een bissectrice is. En de hoek ADC en de hoek BDC zijn aangrenzende hoeken, en het volgt uit de gelijkheid 2 dat ze allebei recht zijn. Het blijkt dat CD de hoogte is van een driehoek. Dit is het eigendom van de mediaan van een gelijkbenige driehoek.

En nu een beetje over de tekenen van een gelijkbenige driehoek.

Stelling 3

Als in een driehoek twee hoeken gelijk zijn aan elkaar, dan is zo'n driehoek gelijkbenig

Bewijs van de stelling.

Stel dat we een driehoek ABC hebben, waarinhoek CAB = hoek van CBA. Driehoek ABC = driehoek BAC door het tweede teken van gelijkheid tussen driehoeken. Zo is het, omdat AB = BA; hoek CBA = hoek CAB, hoek CAB = hoek CBA. Uit deze gelijkheid van driehoeken hebben we de gelijkheid van de overeenkomstige zijden van de driehoek - AC = BC. Dan blijkt dat de driehoek ABC gelijkbenig is.

Stelling 4

Als in een willekeurige driehoek de mediaan ook de hoogte is, dan is zo'n driehoek gelijkbenig

Bewijs van de stelling.

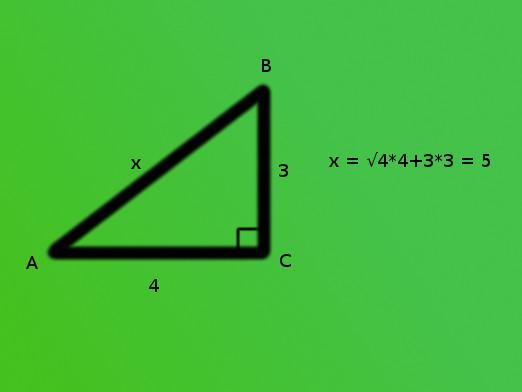
In de driehoek ABC tekenen we de mediaan van de CD. Het zal ook de hoogte zijn. Rechthoekige driehoek ACD = BCD rechthoekige driehoek, aangezien de CD voor hen gangbaar is en de kathode AD = de BD. Hieruit volgt dat hun hypotenusa gelijk is aan elkaar, als de overeenkomstige delen van gelijke driehoeken. Dit betekent dat AB = BC.

Stelling 5

Als de drie zijden van de driehoek gelijk zijn aan de drie zijden van de andere driehoek, dan zijn deze driehoeken gelijk

Bewijs van de stelling.

Stel dat we een driehoek ABC en een driehoek A1B1C1 hebben zodat de zijden AB = A1B1, AC = A1C1, BC = B1C1. We beschouwen het bewijs van deze stelling door tegenspraak.

Laten we aannemen dat deze driehoeken niet gelijk zijn aan elkaaralleen. We hebben dus dat de hoek BAC niet gelijk is aan de hoek B1A1C1, de hoek ABC is niet gelijk aan de hoek A1B1C1, de hoek ACB is niet gelijk aan de hoek A1C1B1 op hetzelfde moment. Anders zouden deze driehoeken volgens het bovenstaande kenmerk gelijk zijn.

Neem aan dat de driehoek A1B1C2 = driehoek isABC. Bij de driehoek ligt de vertex C2 met de vertex C1 ten opzichte van de lijn A1B1 in een halfvlak. We veronderstelden dat de hoekpunten C2 en C1 niet samenvallen. Stel dat het punt D het middelpunt is van C1C2. We hebben dus gelijkbenige driehoeken B1C1C2 en A1C1C2, die een gemeenschappelijke basis C1C2 hebben. Het blijkt dat hun medianen B1D en A1D ook hun hoogtepunten zijn. Dit betekent dat de rechte B1D en de rechte lijn A1D loodrecht staan ​​op de rechte lijn C1C2.

B1D en A1D hebben verschillende punten B1 en A1 en kunnen bijgevolg niet samenvallen. Maar in feite kunnen we door het punt D van C1C2 slechts één rechte lijn loodrecht daarop tekenen. We hebben een tegenspraak.

Nu weet je wat de eigenschappen van een gelijkbenige driehoek zijn!