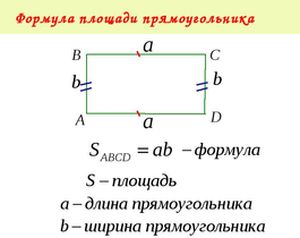
Hoe het gebied van een driehoek te vinden?

Wiskunde is een complexe wetenschap die memoriseren vereist en het vermogen om met een groot aantal formules te werken. Laten we een concrete situatie bekijken, voor je de taak: vind het gebied van de driehoek ABC. Waar te beginnen?

Voor elk probleem van dit type, het schemaacties: selecteer wat is gegeven (type driehoek, gegeven elementen, enz.) - kies een geschikte formule waarmee je het antwoord uit de brongegevens kunt vinden. Laten we dus de meest voorkomende formules selecteren voor het beantwoorden van de vraag hoe het gebied van een driehoek te vinden is:

1. Bekend ten minste één zijde van de driehoek en de hoogte ervan. In dit geval de klassieke formule S = ah / 2. Hier is a de lengte van de zijde van de driehoek genomen als de basis, h is de lengte van de hoogte van de driehoek. Het is belangrijk om de hoogte te kiezen die naar de basis wordt verlaagd.
2. Er zijn twee zijden van de driehoek en de hoek ertussen. De formule werkt S = a * b * sin (β) / 2. Hier a, b zijn de bekende lengtes van de zijden van de driehoek, β is de grootte van de hoek daartussen.
3. Alle drie zijden van de driehoek zijn bekend. De formule van Heron helpt hier S = √ (p * (p-s1) * (p-s2) * (p-s3)). Hier zijn sl, s2, s3 de zijden van de driehoek, p is de semiperimeter. Om een ​​halve meter te vinden, moeten we de lengtes van alle zijden van de driehoek optellen en de som in twee delen verdelen.
4. Om het gebied van een rechthoekige driehoek te vinden,Het is noodzakelijk om het product van de lengte van de poten in tweeën te delen. Deze regel wordt gebruikt om problemen op te lossen bij het vinden van het gebied van de driehoek dat zich al in het vierde leerjaar van de school bevindt. Als een rechthoekige driehoek wordt gegeven, gebruiken we de formule om het gebied te berekenen S = ab / 2. Hier a, b zijn de benen.
5. Om het gebied van een gelijkbenige te berekenendriehoek is van toepassing op de formule van clausule 1 - clausule 3. Bovendien kan in de formule 1 bisectrix, naast de hoogte en de mediaan, fungeren als de parameter h; alle elementen zijn gelijk.
6. Als de coördinaten van de hoekpunten van een driehoek bekend zijn in het vlak, gebruiken we de formule
   S = | (Bx-Ax) (Cy-Ay) - (Cx-Ax) (By-Ay) | / 2, waarbij de hoekpunten worden gegeven door de coördinaten A (Ax, Ay), B (Bx, By), C (Cx, Cy).
7. Als een gelijkzijdige of regelmatige driehoek met bekende zijde a wordt gegeven in de probleemformule S = 2a * √3 / 4.
8. Het gebied van de veelzijdige driehoek is te vinden met behulp van alle formules, met uitzondering van hoofdstuk 5, p7.

Een voorbeeld. Vind het gebied en het vierkant voor de rechter driehoek met zijde 2. We werken aan het item 7: S = 2 * 2 * √3 / 4 = √3 (eenheden²). S²= 3.

Het blijft om op te merken dat op de vermelde optiesde lijst eindigt niet. Er zijn een groot aantal formules om het gebied van een driehoek te vinden. Elke taak vereist een zorgvuldige analyse van de conditie, waarbij de benodigde gegevens worden gemarkeerd om de juiste oplossing te kiezen. Veel succes met deze zoekopdracht.