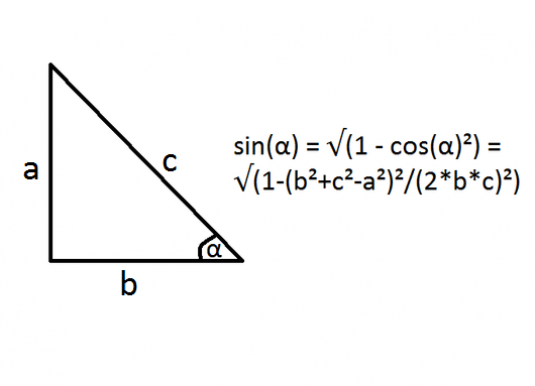Hoe een akkoord te vinden?

Een akkoord in een cirkel vinden, in essentie -dit is een wiskundig probleem, en nog specifieker, het probleem is van het gedeelte van de geometrie. Dat is de reden waarom het gebruik van reeds bekende en bewezen formules gewoon noodzakelijk is. Bovendien moet je de bekende grootheden, de eigenschappen van de meest verschillende constructies in de cirkel en de elementen ervan kennen, pas dan zal het vereiste segment dat twee willekeurige punten op het oppervlak van dezelfde cirkel verbindt, een akkoord genoemd, worden gedefinieerd.

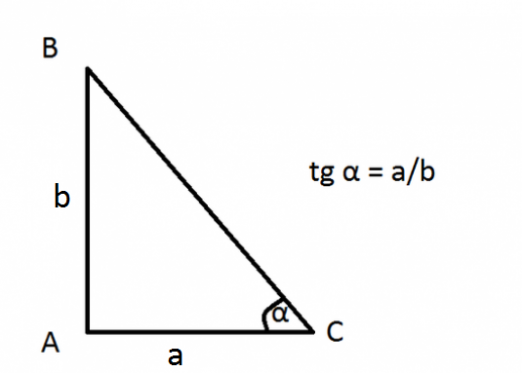
De verbinding van twee punten op een cirkel door een rechte lijn is een akkoord. Het langste akkoord van een cirkel is dus de diameter. Dit akkoord gaat door het midden van een gegeven cirkel.

Een akkoord vinden

Om te weten hoe je een akkoord kunt vinden, de lengte L,het is gebruikelijk om de formule L = 2R · sin (x / 2) te gebruiken. Als je dit probleem op een toegepaste manier oplost, dan heb je een Gon, Liniaal en Gradenboog nodig. Met hun hulp worden de lengte van de aanhaalboog, de straal van de gegeven cirkel en de hoek tussen de stralen die naar de uiteinden van het akkoord werden getrokken bepaald.

Om duidelijker weer te geven hoe u de lengte kunt vindenakkoorden, kunt u een voorbeeld gebruiken waarbij het midden van de cirkel 0 is, er is een akkoord-AB, een hoek tussen de stralen OA en OB-x, de straal van de cirkel R en de hoek x zijn bekend. De gevormde driehoek ABO is gelijkbenig omdat OA = OB = R. Met de formule AB = 2 * R * sin (x / 2) wordt de koordelengte AB verkregen.

Een ander voorbeeld, met andere bekendeparameters, zal helpen om te begrijpen hoe het akkoord van de cirkel te vinden. Parameters: cirkelradius R, DIA lengte bij het koppelen boog, waarbij punt C op de omtrek van het midden van A en B. De formule is x gedefinieerd door de hoek in graden: x = (ACB * 180) / (pi * R). Het blijft alleen vervanger in deze uitdrukking het eerder afgeleide van de vereiste koordlengte: AB = 2 * R * sin ((ACB * 90) / (pi * R)).

Op deze voorbeelden kan worden begrepen dat het kennen van de parameters van de twee grootheden die nodig zijn voor het berekenen van de akkoordlengte, het substitueren ervan in de formule, de derde, de onbekende hoeveelheid, ook wordt bepaald.

Het derde voorbeeld is wanneer de hoek bekend is en ooklengte van de boog. De straal R is onbekend. Het is gelijk aan (ACB * 180) / (pi * x). Nu moet de verkregen uitdrukking worden vervangen door de formule voor het bepalen van de lengte van het akkoord: AB = ((ACB * 360) / (pi * x)) * sin (x / 2). Nu weet je welk akkoord er is en hoe je het kunt vinden. Dit zal u helpen bij het oplossen van een wiskundig en geometrisch probleem.