Hoe de biquadratische vergelijking op te lossen?

Alvorens over te gaan tot de oplossing van de bikwadraats vergelijking, het helpt om te begrijpen hoe het eruit ziet en hoe het verschilt van de klassieke vierkantsvergelijking. De vergelijking van de vormbijl4 + bx2 + c = 0 heet biquadratic met éénvariabele (algebraïsche vergelijking van de vierde graad). Om de vergelijking naar de vierkante vorm te brengen en via de discriminant op te lossen, is het noodzakelijk om de substitutie van de variabele te gebruiken:
- dat is: x2 = t
En dan hebben we de standaardvergelijking van het formulier op2 + bt + c = 0
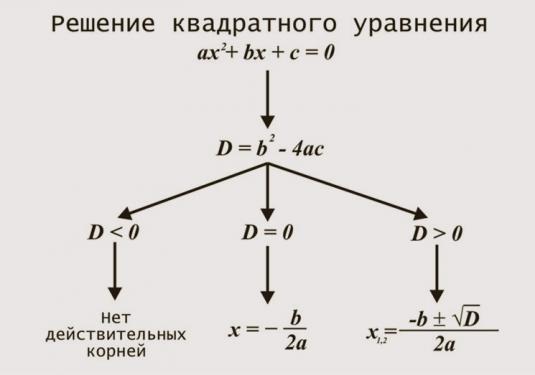
De discriminant wordt berekend met de formule D = b2 - 4ac.
- In het geval dat D = 0, heeft de vergelijking één enkele wortel t1 = -b / 2a, en hieruit verkrijgen we de vereiste oplossing van onze vergelijking x = sqrt (t1).
- Als D> 0 heeft de vergelijking twee wortels t1 = (-b + sqrt (D)) / 2a en t2 = (-b - sqrt (D)) / 2a. Vergeet de ingevoerde variabele niet en we krijgen een eindige oplossing x1,2 = sqrt (t1) en x3,4 = sqrt (t2)
Belangrijke opmerking: als een van de waarden van tik <0, dan voor D = 0 heeft de initiële biquadratische oplossing geen echte wortels en voor D> 0 is er hoogstens één enkele echte wortel.
Het gebruik van de Vieta-stelling
Het is nuttig om te weten: in het geval dat we de gereduceerde kwadratische vergelijking hebben (coëfficiënt op t2 = 1), is de stelling van Vieta van toepassing en is het zoeken naar een oplossing beperkt tot een minimum aan acties:
- t1 + t2 = -b
- t1 * t2 = c
Laten we een voorbeeld bekijken:
- X4 - 3x2 + 2 = 0
gebruikmakend van de verandering van variabele x2 = t, we brengen de kwadratische vergelijking naar de vorm t2 - 3t; + 2 = 0.
- D = (-3)2 - 4 * 1 * 2 = 1.
De wortels van de kwadratische vergelijking t1 = 2, t2 = 1.
Rekening houdend met de geïntroduceerde verandering van variabele, verkrijgen we de oplossing van de vereiste biquadratische vergelijking: t1 = sqrt (2); t2 = -sqrt (2); t3 = 1; t4 = -1.
Voor deze taak kunnen we de stelling van Viet toepassen, aangezien de coëfficiënt van de variabele met de hoogste graad 1 is:
- t1 + t2 = 3
- t1 * t2 = 2
Vandaar t1 = 2, t2 = 1. Zoals we zien, vallen de wortels van de kwadratische vergelijking in beide gevallen samen, en daarom zal de oplossing van de biquadratische vergelijking hetzelfde zijn.
In dit artikel hebben we een speciaal geval overwogen van het oplossen van een biquadratische vergelijking, die niet ingewikkelder is opgelost dan de klassieke kwadratische vergelijking.