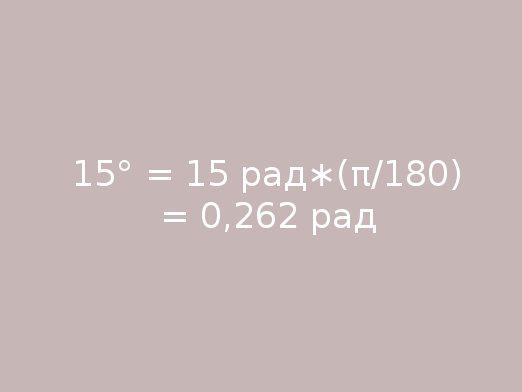Hoe een aangrenzende hoek te vinden?

Bekijk de video

Wiskunde is de oudste exacte wetenschap dieverplichte studie op scholen, hogescholen, instituten en universiteiten. Basiskennis wordt echter altijd op school gelegd. Soms wordt een kind een tamelijk moeilijke taak gesteld en kunnen ouders niet helpen, omdat ze sommige dingen uit de wiskunde gewoon zijn vergeten. Bijvoorbeeld hoe de aangrenzende hoek te vinden in termen van de waarde van de basishoek, enzovoort. De taak is eenvoudig, maar het kan problemen veroorzaken bij het oplossen vanwege onwetendheid over hoe hoeken naast elkaar worden genoemd en hoe je ze kunt vinden.
Laten we de definitie en eigenschappen van aangrenzende hoeken gedetailleerder bekijken, evenals hoe ze uit de gegevens in het probleem kunnen worden berekend.
De definitie en eigenschappen van aangrenzende hoeken
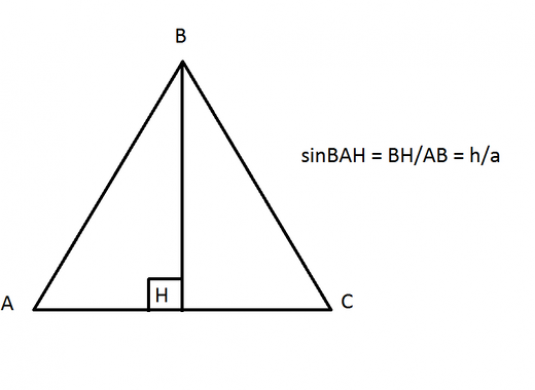
Twee stralen die afkomstig zijn van een enkele punt vormeen figuur genaamd "vlakke hoek". Dit punt wordt de top van de hoek genoemd, en de stralen zijn de zijkanten. Als we een van de stralen voorbij het startpunt langs een rechte lijn voortzetten, wordt een andere hoek gevormd, die aangrenzend wordt genoemd. Bij elke hoek zijn er in dit geval twee aangrenzende hoeken, omdat de zijden van de hoek equivalent zijn. Dat wil zeggen, er is altijd een aangrenzende hoek van 180 graden.
De basiseigenschappen van aangrenzende hoeken zijn
- Aangrenzende hoeken hebben een gemeenschappelijke vertex en één zijde;
- De som van de aangrenzende hoeken is altijd 180 graden of het getal Pi, als de berekening wordt uitgevoerd in radialen;
- Sines van aangrenzende hoeken zijn altijd gelijk;
- De cosinussen en raaklijnen van de aangrenzende hoeken zijn gelijk, maar ze hebben tegengestelde tekens.
Vanwege deze eigenschappen is het vrij eenvoudig om de aangrenzende hoek te berekenen, wetende sommige gegevens.
Hoe aangrenzende hoeken te vinden
Gewoonlijk worden drie variaties van het probleem van het vinden van de waarde van aangrenzende hoeken gegeven
- De waarde van de basishoek wordt gegeven;
- De verhouding van de hoofd- en aangrenzende hoek wordt gegeven;
- De waarde van de verticale hoek wordt gegeven.
Elke versie van het probleem heeft zijn eigen oplossing. Overweeg hen.
De waarde van de basishoek
Als de taak de waarde van de basishoek opgeeft, danhet vinden van een aangrenzende hoek is heel eenvoudig. Hiervoor is het voldoende om de waarde van de basishoek af te trekken van 180 graden en krijgt u de waarde van de aangrenzende hoek. Deze oplossing is gebaseerd op de eigenschap van een aangrenzende hoek - de som van de aangrenzende hoeken is altijd 180 graden.
Als echter de waarde van de basishoek wordt gegeven in radialen ennodig om een taak aangrenzende hoek in radialen, dan worden afgetrokken van de Pi basishoekwaarde vinden, omdat een volledige schaalwaarde van de hoek van 180 graden is gelijk aan het getal Pi.
Gegeven de verhouding van de hoofd- en aangrenzende hoek
In het probleem kan de verhouding van de hoofd- en de aangrenzende hoek worden gegeven in plaats van graden en de radialen van de waarde van de basishoek. In dit geval zal de oplossing eruitzien als de verhoudingsverhouding:
- We geven de proportie van de proportie van de hoofdhoek aan, als de variabele "Y".
- We geven de breuk gerelateerd aan de aangrenzende hoek aan als de variabele "X".
- Het aantal graden dat op elke verhouding valt, we geven bijvoorbeeld 'a' aan.
- De algemene formule ziet er als volgt uit: a * X + a * Y = 180 of een * (X + Y) = 180.
- We vinden de gemeenschappelijke factor van de vergelijking "a" met de formule a = 180 / (X + Y).
- Vervolgens wordt de resulterende waarde van de gemeenschappelijke factor "a" vermenigvuldigd met de fractie van de nader te bepalen hoek.
We kunnen dus de waarde van de naastgelegen vindenhoek in graden. Als u echter de waarde in radialen wilt vinden, hoeft u alleen maar de graden om te zetten in radialen. Om dit te doen, vermenigvuldig je de hoek in graden met het getal Pi en verdeel alles 180 graden. De resulterende waarde zal in radialen zijn.
De waarde van de verticale hoek
Als de taak niet de waarde van de basishoek geeft, maar de waarde van de verticale hoek geeft, bereken dan de aangrenzende hoek met dezelfde formule als in de eerste alinea, waar de waarde van de basishoek wordt gegeven.
De verticale hoek is de hoek die ontstaatHetzelfde punt als het hoofdpunt, maar het is precies in de tegenovergestelde richting gericht. Dit levert een spiegelbeeld op. Dit betekent dat de verticale hoek in grootte gelijk is aan de hoofdhoek. Op zijn beurt is de aangrenzende hoek van de verticale hoek gelijk aan de aangrenzende hoek van de basishoek. Hierdoor is het mogelijk om de aangrenzende hoek van de basishoek te berekenen. Om dit te doen, trekt u eenvoudig de waarde van de verticaal van 180 graden af en krijgt u de waarde van de aangrenzende hoek van de hoofdhoek in graden.
Indien de waarde wordt uitgedrukt in radialen, dan worden afgetrokken van de pi-waarde van de verticale hoek, als de waarde van de totale geëxpandeerde hoek van 180 graden gelijk is aan het getal Pi is.
Ook kunt u onze nuttige artikelen lezen. Wat is de hoek en Wat zijn de hoeken.