Hoe de correlatiecoëfficiënt te vinden?

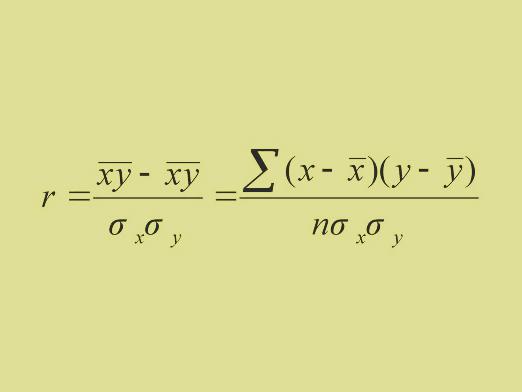
In wiskundige statistieken is de correlatiestatistische en probabilistische afhankelijkheid, die geen strikt functioneel karakter heeft. Correlatie afhankelijkheid verschijnt in het geval dat een van de tekens afhankelijk is van zowel de gegeven seconde als een aantal andere willekeurige factoren. De correlatiecoëfficiënt dient als een mathematische maat voor de afhankelijkheid van twee willekeurige variabelen.

Typen correlatiecoëfficiënten kunnen zijnnegatief en positief. Berekeningen uitgevoerd met behulp van correlatie zijn niet erg ingewikkeld, maar vereisen speciale zorg van de uitvoerder in de berekeningen. Met deze berekeningen heeft u zeker een technische rekenmachine nodig. Voordat u uitzoekt hoe u de correlatiecoëfficiënt kunt vinden, moet u de betekenis van de waarden van de coëfficiënten begrijpen:

• In het geval dat de waarde van de modulus dichter bij 1 ligt, is dit een directe indicator van de aanwezigheid van sterke koppeling.
• Als de waarde dichter bij 0 ligt, betekent dit al een zwakke verbinding of zelfs de afwezigheid ervan.
• Wanneer de correlatiecoëfficiënt 1 is, dan hebben we het over een functionele verbinding, die de mogelijkheid aangeeft om met een wiskundige functie de verandering van twee grootheden te beschrijven.

De volgorde en methode voor het berekenen van de correlatiecoëfficiënt

Om de selectieve correlatiecoëfficiënt te vinden, kunt u twee methoden gebruiken:

• rangmethode, of Spearman's methode,
• de methode van vierkanten, of de Pearson-methode.

Rangorde methode

De rangmethode is het volgende algoritme van acties:

1. Het is vereist om twee rijen te maken die uit gepaarde paren bestaanovereenkomende attributen. In dit geval introduceren we de volgende notatie: de eerste rij is x en de tweede rij is y. De eerste reeks kenmerken moet in stijgende of dalende volgorde worden weergegeven. De numerieke waarden van de tweede rij staan ​​tegenover de waarden van de eerste rij.
2. Vervolgens vervangen we in elk van de vergelijkingsreeksenvolgnummer (rang) de waarde van het kenmerk. Getallen (rangen) duiden de plaatsen van indicatoren of waarden van de eerste en tweede rij aan. En de numerieke waarden van het tweede kenmerk moeten worden toegewezen aan de rangorde in exact dezelfde volgorde als bij de verdeling van het eerste kenmerk naar hun waarden. Er moet rekening mee worden gehouden dat als het kenmerk in de reeks dezelfde waarden heeft, de rangen moeten worden bepaald als het gemiddelde van de som van de volgnummers van deze grootheden.
3. Vervolgens bepalen we het verschil in rang tussen de indicatoren: (d) = x-y.
4. Daarna hebben we het verkregen verschil in rangen (d²).
5. En tenslotte krijgen we de som van de vierkanten van het verschil, waarna we alle verkregen waarden in de volgende formule vervangen: Pxy = 1- (6 Σd²) / n (n²-1).

Methode van vierkanten

De methode van vierkanten omvat het volgende algoritme:

1. Om de correlatiecoëfficiënt te vindenin het begin is het nodig om variatieresultaten te construeren voor elk van de attributen die worden vergeleken. Geef de eerste rij aan - x en de tweede rij - y. Nu bepalen we de gemiddelde waarden (M₁ en M₂) voor elke variatieserie.
2. Vervolgens vinden we de afwijkingen van elke numerieke waarde (d_X en d_Y) van de gemiddelde waarde van de serie.
3. We vermenigvuldigen de verkregen afwijkingen en construeren elke afwijking in het vierkant en tellen vervolgens over elke rij.
4. Dan is het noodzakelijk om alle eerder in de formule verkregen waarden te vervangen en zo de correlatiecoëfficiënt te vinden: r_xy = Σ (dx * dy) / (sqrt (Σ d2x) * Σ d2y).
5. Als er een computertechnologie is, kan de berekening worden gemaakt met behulp van de volgende formule, ook deze berekeningsvorm kan worden gebruikt in programma's die zijn geschreven in de Pascal-taal:_xy= (nΣxy- / Σx * Σy) / (sqrt ([nΣx²- Σx²] - [nΣy²- Ja²])).